图像标定全解析：历史、方法与计算原理

在计算机视觉、工业检测、无人驾驶等领域，图像标定（Camera Calibration）是获取高精度图像空间与物理空间对应关系的基础环节。本文将从历史发展、常用标定方法及其计算过程三个方面进行详细介绍。

一、图像标定的历史

图像标定的概念起源于计算机视觉早期对相机成像模型的研究。相机标定的目标是确定相机内部参数（Intrinsic Parameters）和外部参数（Extrinsic Parameters），以便将二维图像坐标与三维世界坐标建立映射关系。其发展历程大致如下：

20 世纪 80 年代
- 初期标定主要依赖手工测量和物理几何模型。
- Tsai（1987）提出了经典的两步标定法，将相机的内参和外参分开估计。
90 年代
- 张正友（Zhang Zhengyou, 1999）提出基于平面棋盘格的灵活标定方法，可通过多幅平面图像计算相机内参、畸变参数和外参，大大简化了标定流程。
- 该方法引入了线性初值 + 非线性优化，提高了精度和鲁棒性。
21 世纪
- 随着工业视觉和机器视觉的发展，标定方法不断优化，支持多相机系统、鱼眼相机、结构光等场景。
- 自动化、快速、无需人工干预的标定方法逐渐成为研究热点。

总结：图像标定从早期依赖物理测量逐步发展为利用标准图案（棋盘格、圆点阵列）和数学优化方法实现自动化和高精度。

二、图像标定的常用方法

根据标定对象和方法的不同，常用标定方法可分为以下几类：

1. 几何法（Direct Geometric Method）

基本思路：利用已知三维物理坐标和对应图像坐标，通过解析几何关系求解相机参数。
特点：适用于标定板位置固定、三维坐标已知的场景。
计算过程：
1. 建立相机投影模型：
  $$
  s \begin{bmatrix}u \ v \ 1\end{bmatrix} = K [R|t] \begin{bmatrix}X \ Y \ Z \ 1\end{bmatrix}
  $$
  其中，K 为内参矩阵，[R|t] 为外参。
2. 将每个已知点对形成线性方程组。
3. 用最小二乘法求解未知参数。
4. 可选：使用非线性优化（如 Levenberg-Marquardt）进一步优化重投影误差。

2. 平面标定法（Planar Pattern Method）

代表方法：张正友标定法（Zhang, 1999）。
核心思想：利用平面棋盘格图像的多幅姿态，估计单应性矩阵，再解内参和畸变参数。
计算过程：
1. 对每幅棋盘格图像，计算每个角点在图像上的像素坐标 `(u,v)。
2. 假设世界平面 Z=0，建立平面到像素的单应性矩阵：
  $$
  s \begin{bmatrix}u \ v \ 1\end{bmatrix} = H \begin{bmatrix}X \ Y \ 1\end{bmatrix}
  $$
3. 通过最少四个点解出每幅图像的 HHH。
4. 利用多幅图像的 HHH 联立求解相机内参 KKK。
5. 根据内参，进一步求解外参 R,tR, tR,t。
6. 使用非线性优化最小化重投影误差，计算畸变参数：
  - 径向畸变：
    $$
    u_d = u(1 + k_1 r^2 + k_2 r^4 + …)
    $$
  - 切向畸变：
    $$
    u_d = u + [2p_1 uv + p_2(r^2 + 2u^2)]
    $$

3. 自标定法（Self-Calibration）

基本思路：利用运动或场景约束，不需要标定板，通过图像特征匹配估计相机参数。
适用场景：SLAM、Structure-from-Motion（SfM）。
计算方法：
1. 对多幅图像进行特征匹配（如 SIFT、ORB）。
2. 根据本质矩阵 E 或基础矩阵 F 解外参。
3. 假设内参恒定，逐步优化（bundle adjustment）求出完整相机参数。

4. 标定板/圆点阵列法

与平面棋盘格类似，但用对称圆点阵列，提高亚像素定位精度。
对点中心检测后，解单应性或投影矩阵求相机参数。

三、图像标定的计算原理

1. 相机模型

常用的针孔相机模型：
$$
s \begin{bmatrix}u\v\1\end{bmatrix} = \begin{bmatrix}f_x & \gamma & c_x\ 0 & f_y & c_y\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}R & t\ 0 & 1\end{bmatrix} \begin{bmatrix}X\Y\Z\1\end{bmatrix}
$$

$$
K = \begin{bmatrix}f_x & \gamma & c_x\ 0 & f_y & c_y\ 0 & 0 & 1\end{bmatrix}
$$

：内参矩阵
- $$
  f_x, f_y：焦距（像素单位）
  $$
- $$
  (c_x, c_y)：主点坐标
  $$
- $$
  \gamma：像素非正交因子
  $$
R, t：外参，描述相机姿态与位置

2. 标定求解步骤（以张正友法为例）

检测特征点：棋盘角点或圆点中心。
单应性求解：对每幅图像构建线性方程，求 HHH。
内参求解：利用多幅 HHH 联立求解 KKK。
外参求解：利用 HHH 与 KKK 解出 R,tR, tR,t。
畸变优化：通过非线性优化最小化重投影误差，估计径向与切向畸变参数。

非线性优化常用公式：

$$
\min \sum_i | \mathbf{x}_i - \hat{\mathbf{x}}_i(K, R, t, k_1, k_2, p_1, p_2) |^2
$$

四、总结

图像标定历史：从手工几何法 → 平面棋盘格标定 → 自动化、支持畸变和多相机。
常用方法：
- 几何法（解析或最小二乘）
- 平面棋盘格标定（Zhang方法）
- 圆点阵列、亚像素优化
- 自标定法（无标定板，依赖多图像匹配）
计算核心：
- 建立像素坐标与世界坐标映射
- 线性求解初值（单应性或投影矩阵）
- 非线性优化（最小化重投影误差）得到最终参数

标定完成后，可以将像素坐标精确转换为物理坐标，实现工业测量、三维重建和机器视觉的高精度应用。

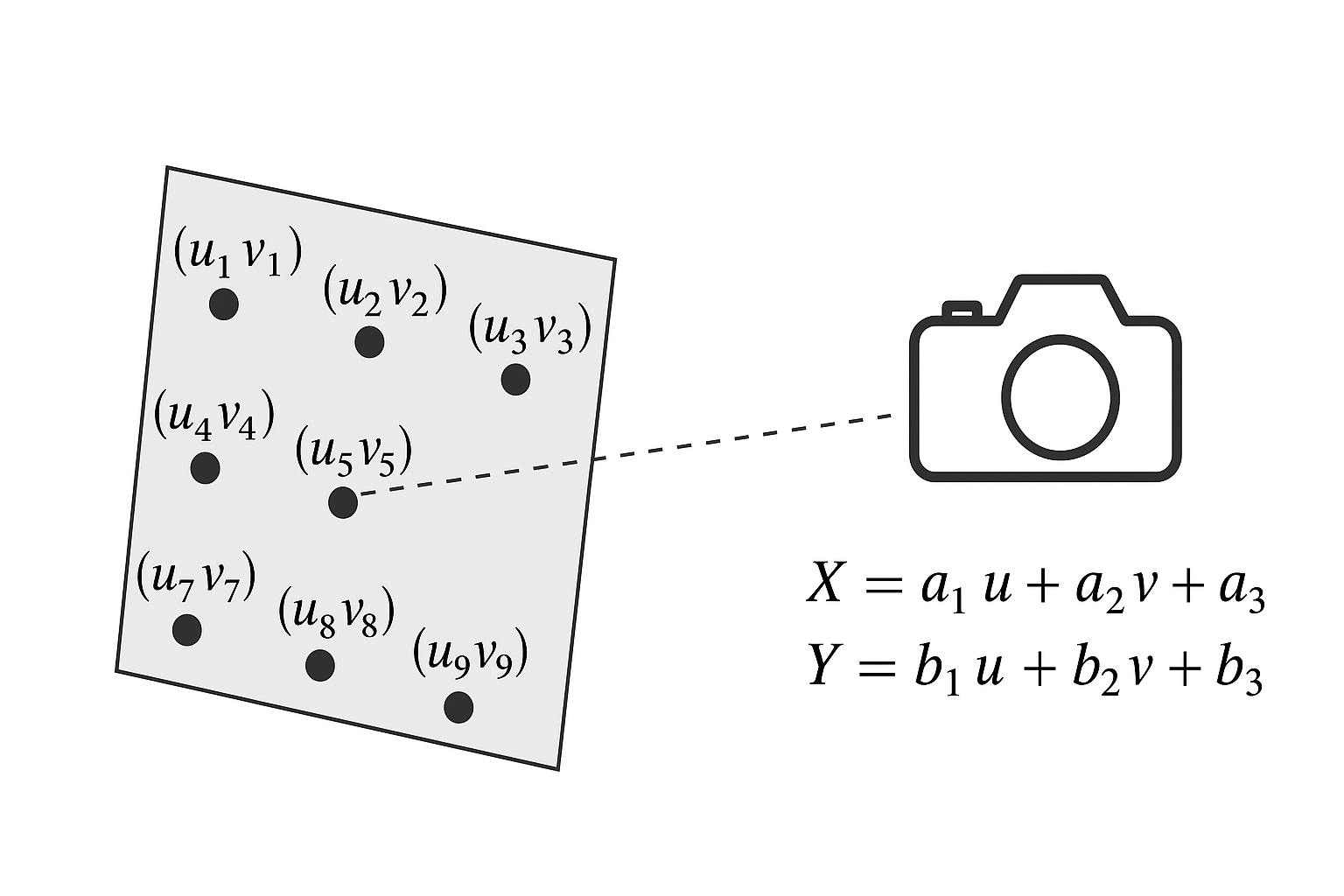
五、以九点标定法为例 -九点标定法（Nine-Point Calibration）详解

在工业视觉或机器视觉中，当目标场景是平面且相机畸变较小，可以用 九点标定法 通过少量已知点快速估计相机的标定矩阵（仿射或透视），用于将像素坐标转换为物理坐标。

一、基本原理

九点标定法通常假设：

相机成像满足针孔模型或近似仿射投影：
$$
\begin{bmatrix}X\Y\end{bmatrix} \approx \begin{bmatrix}a_1 & a_2 & a_3\ b_1 & b_2 & b_3\end{bmatrix} \begin{bmatrix}u\v\1\end{bmatrix}
$$
- (u,v)：图像像素坐标
- (X,Y)：对应机械坐标（实际物理坐标）
- a_1,a_2,a_3,b_1,b_2,b_3：待求仿射系数
如果考虑透视畸变，可用 3×3 单应性矩阵：
$$
s \begin{bmatrix}u\v\1\end{bmatrix} = \begin{bmatrix}h_{11} & h_{12} & h_{13}\ h_{21} & h_{22} & h_{23}\ h_{31} & h_{32} & 1\end{bmatrix} \begin{bmatrix}X\Y\1\end{bmatrix}
$$
至少需要 3 个点解仿射矩阵，4 个点解透视矩阵，但九点标定提供更多点用于最小二乘优化，提高鲁棒性。

二、九点标定法的计算步骤（仿射模型）

步骤 1：收集像素与机械坐标

准备 9 个已知对应点
$$
(u_i,v_i) \leftrightarrow (X_i,Y_i)
$$
，一般分布在整个工作区域，保证标定精度。

步骤 2：建立线性方程组

仿射模型方程：
$$
\begin{cases} X_i = a_1 u_i + a_2 v_i + a_3 \ Y_i = b_1 u_i + b_2 v_i + b_3 \end{cases}
$$
可改写为矩阵形式：
$$
\underbrace{\begin{bmatrix} u_1 & v_1 & 1\ \vdots & \vdots & \vdots\ u_9 & v_9 & 1 \end{bmatrix}}_{9\times3} \begin{bmatrix}a_1\a_2\a_3\end{bmatrix} = \begin{bmatrix}X_1\\vdots\X_9\end{bmatrix}, \quad \begin{bmatrix} u_1 & v_1 & 1\ \vdots & \vdots & \vdots\ u_9 & v_9 & 1 \end{bmatrix} \begin{bmatrix}b_1\b_2\b_3\end{bmatrix} = \begin{bmatrix}Y_1\\vdots\Y_9\end{bmatrix}
$$

步骤 3：最小二乘求解

由于 9 个方程大于 3 个未知量，可以使用最小二乘法求解：
$$
\mathbf{a} = (U^T U)^{-1} U^T \mathbf{X}, \quad \mathbf{b} = (U^T U)^{-1} U^T \mathbf{Y}
$$
得到仿射系数 (a_1,a_2,a_3,b_1,b_2,b_3)

步骤 4：像素当量计算

计算单位像素对应的物理长度（mm/px）：
$$
s_u = \sqrt{a_1^2 + b_1^2}, \quad s_v = \sqrt{a_2^2 + b_2^2}
$$
这给出了沿水平（u）和垂直（v）方向的标定比例。

步骤 5：坐标转换

任意像素点 (u,v)(u,v)(u,v) 可直接转换为机械坐标：
$$
3X = a_1 u + a_2 v + a_3, \quad Y = b_1 u + b_2 v + b_3
$$

三、九点标定法（透视模型）计算

当场景存在透视畸变时，需要用 单应性矩阵 H：

对每一点建立投影关系：

$$
s \begin{bmatrix}u_i\v_i\1\end{bmatrix} = \begin{bmatrix}h_{11} & h_{12} & h_{13}\ h_{21} & h_{22} & h_{23}\ h_{31} & h_{32} & 1\end{bmatrix} \begin{bmatrix}X_i\Y_i\1\end{bmatrix}
$$

展开成 2 个方程（X和Y）：

$$
\begin{cases} h_{11} X_i + h_{12} Y_i + h_{13} - u_i(h_{31} X_i + h_{32} Y_i + 1) = 0\ h_{21} X_i + h_{22} Y_i + h_{23} - v_i(h_{31} X_i + h_{32} Y_i + 1) = 0 \end{cases}
$$

对 9 个点，形成 18×8 的线性方程组，用最小二乘法求解 h11,…,h32h_{11},\dots,h_{32}h11,…,h32，并固定 h_{33}=1
透视变换：

$$
X = \frac{h_{11} u + h_{12} v + h_{13}}{h_{31} u + h_{32} v + 1}, \quad Y = \frac{h_{21} u + h_{22} v + h_{23}}{h_{31} u + h_{32} v + 1}
$$

局部像素当量可用雅可比矩阵计算：

$$
\frac{\partial X}{\partial u}, \frac{\partial X}{\partial v}, \frac{\partial Y}{\partial u}, \frac{\partial Y}{\partial v}
$$

四、九点标定法特点

优点：
- 少量点即可完成标定，适合小型工作区域或工业检测。
- 计算简单，可用 Excel 或 Matlab 实现。
局限：
- 精度受点位置影响，最好均匀覆盖工作区域。
- 仿射模型不适合大透视畸变场景，需要单应性或非线性优化。

五、小结

九点标定法是工业视觉中快速标定的一种经典方法：

仿射模型：适合小视场、畸变小，计算简便。
透视单应性模型：适合有透视畸变的平面场景，通过最小二乘求解 8 个未知数，可得到局部像素当量。
计算步骤核心：建立线性方程 → 最小二乘求解 → 坐标转换 → 像素当量计算。

什么是图像标定，图像标定在算什么？以九点标定为例